A continuous-wave goes on continuously without any intervals and it is the baseband message signal, which contains the information. This wave has to be modulated.
According to the standard definition, “The amplitude of the carrier signal varies in accordance with the instantaneous amplitude of the modulating signal.” Which means, the amplitude of the carrier signal containing no information varies as per the amplitude of the signal containing information, at each instant. This can be well explained by the following figures.
Advertisement
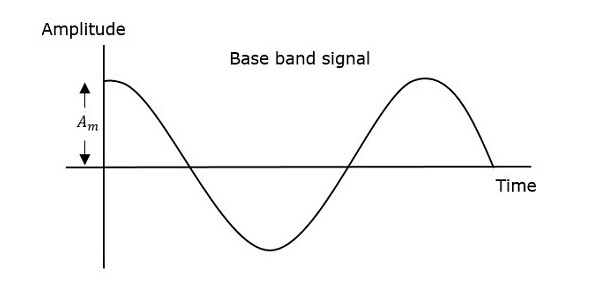
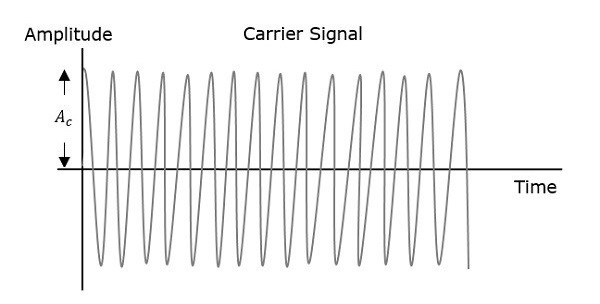

The first figure shows the modulating wave, which is the message signal. The next one is the carrier wave, which is a high frequency signal and contains no information. While, the last one is the resultant modulated wave.
It can be observed that the positive and negative peaks of the carrier wave, are interconnected with an imaginary line. This line helps recreating the exact shape of the modulating signal. This imaginary line on the carrier wave is called as Envelope. It is the same as that of the message signal.
Mathematical Expressions Of Amplitude Madulation
Advertisement
Following are the mathematical expressions for these waves.
Time-domain Representation of the Waves (Amplitude Modulation)
Advertisement
Let the modulating signal be,m(t)=Amcos(2πfmt)m(t)=Amcos(2πfmt)
and the carrier signal be,c(t)=Accos(2πfct)c(t)=Accos(2πfct)
Where,
AmAm and AcAc are the amplitude of the modulating signal and the carrier signal respectively.
Advertisement
fmfm and fcfc are the frequency of the modulating signal and the carrier signal respectively.
Then, the equation of Amplitude Modulated wave will be
s(t)=[Ac+Amcos(2πfmt)]cos(2πfct)s(t)=[Ac+Amcos(2πfmt)]cos(2πfct) (Equation 1)
Modulation Index
A carrier wave, after being modulated, if the modulated level is calculated, then such an attempt is called as Modulation Index or Modulation Depth. It states the level of modulation that a carrier wave undergoes.
Rearrange the Equation 1 as below.
s(t)=Ac[1+(AmAc)cos(2πfmt)]cos(2πfct)s(t)=Ac[1+(AmAc)cos(2πfmt)]cos(2πfct)
⇒s(t)=Ac[1+μcos(2πfmt)]cos(2πfct)⇒s(t)=Ac[1+μcos(2πfmt)]cos(2πfct) (Equation 2)
Where, μμ is Modulation index and it is equal to the ratio of AmAm and AcAc. Mathematically, we can write it as
μ=AmAcμ=AmAc (Equation 3)
Hence, we can calculate the value of modulation index by using the above formula, when the amplitudes of the message and carrier signals are known.
Now, let us derive one more formula for Modulation index by considering Equation 1. We can use this formula for calculating modulation index value, when the maximum and minimum amplitudes of the modulated wave are known.
Let AmaxAmax and AminAmin be the maximum and minimum amplitudes of the modulated wave.
We will get the maximum amplitude of the modulated wave, when cos(2πfmt)cos(2πfmt) is 1.
⇒Amax=Ac+Am⇒Amax=Ac+Am (Equation 4)
We will get the minimum amplitude of the modulated wave, when cos(2πfmt)cos(2πfmt) is -1.
⇒Amin=Ac−Am⇒Amin=Ac−Am (Equation 5)
Add Equation 4 and Equation 5.Amax+Amin=Ac+Am+Ac−Am=2AcAmax+Amin=Ac+Am+Ac−Am=2Ac
⇒Ac=Amax+Amin2⇒Ac=Amax+Amin2 (Equation 6)
Subtract Equation 5 from Equation 4.Amax−Amin=Ac+Am−(Ac−Am)=2AmAmax−Amin=Ac+Am−(Ac−Am)=2Am
⇒Am=Amax−Amin2⇒Am=Amax−Amin2 (Equation 7)
Advertisement
The ratio of Equation 7 and Equation 6 will be as follows.AmAc=(Amax−Amin)/2(Amax+Amin)/2AmAc=(Amax−Amin)/2(Amax+Amin)/2
⇒μ=Amax−AminAmax+Amin⇒μ=Amax−AminAmax+Amin (Equation 8)
Therefore, Equation 3 and Equation 8 are the two formulas for Modulation index. The modulation index or modulation depth is often denoted in percentage called as Percentage of Modulation. We will get the percentage of modulation, just by multiplying the modulation index value with 100.
For a perfect modulation, the value of modulation index should be 1, which implies the percentage of modulation should be 100%.
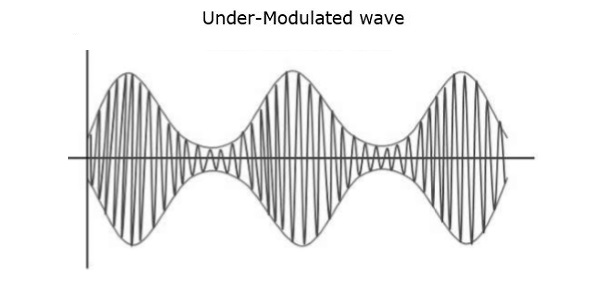
For instance, if this value is less than 1, i.e., the modulation index is 0.5, then the modulated output would look like the following figure. It is called as Under-modulation. Such a wave is called as an under-modulated wave.
If the value of the modulation index is greater than 1, i.e., 1.5 or so, then the wave will be an over-modulated wave. It would look like the following figure.
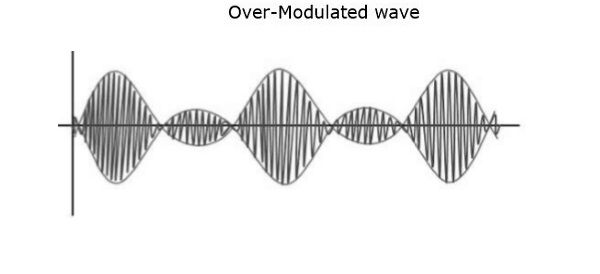
As the value of the modulation index increases, the carrier experiences a 180o phase reversal, which causes additional sidebands and hence, the wave gets distorted. Such an over-modulated wave causes interference, which cannot be eliminated.
Bandwidth of AM (Amplitude Modulation) Wave
Bandwidth (BW) is the difference between the highest and lowest frequencies of the signal. Mathematically, we can write it asBW=fmax−fminBW=fmax−fmin
Consider the following equation of amplitude modulated wave.s(t)=Ac[1+μcos(2πfmt)]cos(2πfct)s(t)=Ac[1+μcos(2πfmt)]cos(2πfct)⇒s(t)=Accos(2πfct)+Acμcos(2πfct)cos(2πfmt)⇒s(t)=Accos(2πfct)+Acμcos(2πfct)cos(2πfmt)
⇒s(t)=Accos(2πfct)+Acμ2cos[2π(fc+fm)t]+Acμ2cos[2π(fc−fm)t]⇒s(t)=Accos(2πfct)+Acμ2cos[2π(fc+fm)t]+Acμ2cos[2π(fc−fm)t]
Hence, the amplitude modulated wave has three frequencies. Those are carrier frequency fcfc, upper sideband frequency fc+fmfc+fm and lower sideband frequency fc−fmfc−fm
Here,
fmax=fc+fmfmax=fc+fm and fmin=fc−fmfmin=fc−fm
Substitute, fmaxfmax and fminfmin values in bandwidth formula.BW=fc+fm−(fc−fm)BW=fc+fm−(fc−fm)⇒BW=2fm⇒BW=2fm
Thus, it can be said that the bandwidth required for amplitude modulated wave is twice the frequency of the modulating signal.
Power Calculations of AM Wave
Consider the following equation of amplitude modulated wave.
s(t)=Accos(2πfct)+Acμ2cos[2π(fc+fm)t]+Acμ2cos[2π(fc−fm)t] s(t)=Accos(2πfct)+Acμ2cos[2π(fc+fm)t]+Acμ2cos[2π(fc−fm)t]
Power of AM wave is equal to the sum of powers of carrier, upper sideband, and lower sideband frequency components.Pt=Pc+PUSB+PLSBPt=Pc+PUSB+PLSB
We know that the standard formula for power of cos signal isP=vrms2R=(vm/2–√)22P=vrms2R=(vm/2)22
Where,
vrmsvrms is the rms value of cos signal.
vmvm is the peak value of cos signal.
First, let us find the powers of the carrier, the upper and lower sideband one by one.
Carrier powerPc=(Ac/2–√)2R=Ac22RPc=(Ac/2)2R=Ac22R
Upper sideband powerPUSB=(Acμ/22–√)2R=Ac2μ28RPUSB=(Acμ/22)2R=Ac2μ28R
Similarly, we will get the lower sideband power same as that of the upper side band power.PLSB=Ac2μ28RPLSB=Ac2μ28R
Now, let us add these three powers in order to get the power of AM wave.Pt=Ac22R+Ac2μ28R+Ac2μ28RPt=Ac22R+Ac2μ28R+Ac2μ28R⇒Pt=(Ac22R)(1+μ24+μ24)⇒Pt=(Ac22R)(1+μ24+μ24)⇒Pt=Pc(1+μ22)⇒Pt=Pc(1+μ22)
We can use the above formula to calculate the power of AM wave, when the carrier power and the modulation index are known.
If the modulation index μ=1μ=1 then the power of AM wave is equal to 1.5 times the carrier power. So, the power required for transmitting an AM wave is 1.5 times the carrier power for a perfect modulation.
Amplitude modulation is mostly used in the form of electronic communication.
1.When it comes to power usage it is not efficient.
2.It requires a very high bandwidth that is equivalent to that of the highest audio frequency.
3.Noise interference is highly noticeable.
1.Amplitude Modulation is easier to implement.
2.Demodulation can be done using few components and a circuit.
3.The receiver used for AM is very cheap.
Need for modulation : –
i) To separate signal from different transmitters :-
Audio frequencies are within the range of 20 Hz to 20 kHz. Without modulation all signals at same frequencies from different transmitters would be mixed up. There by giving impossible situation to tune to any one of them. In order to separate the various signals, radio stations must broadcast at different frequencies.
Each radio station must be given its own frequency band. This is achieved by frequency translation as a result of modulation process.
ii) Size of the antenna : –
For efficient transmission the transmitting antennas should have length at least equal to a quarter of the wavelength of the signal to be transmitted. For an electromagnetic wave of frequency 15 kHz, the wavelength λ is 20 km and one-quarter of this will be equal to 5 km. Obviously, a vertical antenna of this size is impractible. On the other hand, for a frequency of 1 MHz, this height is reduced to 75 m.
Also, the power radiated by an antenna of length l is proportional to (l/λ). This shows that for the same antenna length, power radiated is large for shorter wavelength. Thus, our signal which is of low frequency must be translated to the high frequency spectrum of the electromagnetic wave. This is achieved by the process of modulation.
iii)To Reduce Antenna Height.(practicability of antennas height).
iv)Transmit The Information To long Distance Without interference.
v) Reduce band width.
amlitude modulation
amplitude modulation
amplitude modulation vs frequency modulation
amplitude modulation formula
amplitude modulation circuit
amplitude modulation spectrum
amplitude modulation radio
Advertisement
